Startseite
Geschwindigkeitswerte für das Whitehawk zu niedrig?
Die verwendeten Daten beziehen sich auf eine Whitehawk-Version aus dem Jahr 1996.
Neuere Versionen haben einen noch niedrigeren Luftwiderstand und sind wahrscheinlich mit besser rollenden Reifen ausgestattet.
Geschwindigkeitswerte für das Boardman-Rad zu niedrig?
Die verwendeten Daten gelten für mittelmäßig rauhen Straßenasphalt.
Auf der Bahn eines Velodroms sind die Rollwiderstände i.d.R. deutlich niediger.
Zu hohe Geschwindigkeitswerte / zu niedrige Leistungswerte für den Tieflieger?
Der Rechner auf www.kreuzotter.de verwendet Daten für die Kreuzotter race,
einen sehr schnellen Tieflieger mit steifem Rahmen, effizienter Kraftübertragung zum Hinterrad,
einer Sitzhöhe von nur 17 cm, und einiger aerodynamischen Feinarbeit.
Ihr eigener Tieflieger ist ziemlich wahrscheinlich langsamer...
Mein Rennrad/Tieflieger/Quest rollt bergab viel langsamer als laut Online-Rechner!
Kein Wunder.
Um bei 10 Prozent Gefälle die Endgeschwindigkeit zu erreichen,
müsste ein verschaltes Quest
2 Minuten 33 Sekunden lang bzw. 5.7 km weit ungebremst(!) rollen können,
ein schneller Tieflieger (Kreuzotter race)
1 Minute 54 Sekunden lang bzw. 2.9 km weit,
ein Rennrad (Untenlenkerhaltung)
1 Minute 26 Sekunden lang bzw. 1.54 km weit.
Derart lange und durchgehend steile Gefällestrecken ohne scharfe Kurven dürften in Mitteleuropa einschließlich Alpen schwierig zu finden sein.
Berechnen kann man obige Werte z.B. mit meinem Funktionsgraphplotter WZGrapher (kann gewöhnliche Differentialgleichungen bis zur 5. Ordnung numerisch lösen, kostenlos, momentan nur Windows).
Folgende Bewegungsgleichung berücksichtigt auch die Fahrbahnsteigung, die Änderung der Luftdichte bei Fortbewegung an Steigung/Gefälle und hierbei auch den feuchtadiabatischen vertikalen Temperaturgradienten (hier zu konstant 0.5°/100m angenommen), den normalisierten (neigungsabhängigen) Rollwiderstand, den dynamischen geschwindigkeitsabhängigen Rollwiderstand, und die Windgeschwindigkeit in Fahrtrichtung:
Beschleunigung = (Vortriebskraft - Luftwiderstandskraft - Rollwiderstandskraft - Hangabtriebskraft - dynamische Rollwiderstandskraft) / Masse ,
also:
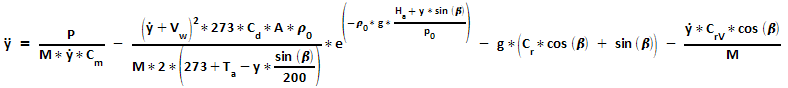
mit:
| y: |
Abhängige Variable: zurückgelegte Wegstrecke [m];
ẏ ist also die Geschwindigkeit, ÿ die Beschleunigung nach einer bestimmten abgelaufenen Zeit |
| P: | Fahrerleistung [W] (für rechnerische Rollversuche auf 0 setzen) |
| Vw: | Windgeschwindigkeit [m/s] (negative Werte: Rückenwind) |
| Ha: | Höhe des Startpunktes über NN [m] |
| Ta: | Lufttemperatur [Grad C] auf Höhe des Startpunktes |
| β: |
Winkel der Fahrbahnsteigung (negative Winkel: Gefälle).
Aus der Fahrbahnsteigung s in Prozent (%) kann dieser Steigungswinkel mit atan(s/100) berechnet werden (je nach eingestelltem Berechnungsmodus in Bogenmaß oder Winkelgrad).
|
| M: | Gesamtmasse Rad + Fahrer [kg] |
| Cd: | Luftwiderstandsbeiwert von Rad+Fahrer |
| A: |
Stirnfläche von Rad+Fahrer [m2].
Näherungswerte für Cd*A, die effektive Stirnfläche, liefert der Geschwindigkeits- & Leistungsrechner |
| Cr: |
Rollwiderstandsbeiwert (ca. 0.0025 bis 0.008)
Näherungswerte liefert der Geschwindigkeits- & Leistungsrechner |
| CrV: | Beiwert für den dynamischen geschwindigkeitsabhängigen Rollwiderstand (näherungsweise 0.1) |
| Cm: | Beiwert (Faktor) für mechanische Verluste (je nach Radtyp zw. 1.03 und 1.09) |
| ρ0: | Luftdichte auf Meereshöhe bei 0° C (1.293 kg/m3) |
| p0: | Luftdruck auf Meereshöhe bei 0° C (101325 Pa) |
| g: | Erdbeschleunigung (9.81 m/s2) |

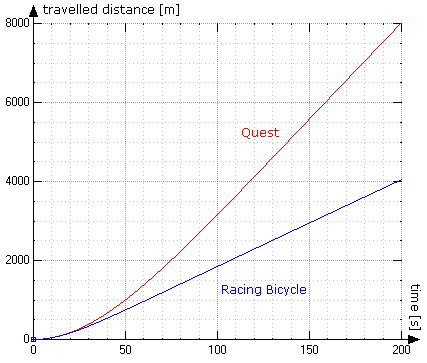
Quest versus Rennrad bei 10% Gefälle, Start bei 800 m über NN (Plot: WZGrapher).
In beiden Diagrammen sieht man schön, dass das erheblich schnellere Rad (das Quest) selbst auf einem Gefälle von 10% erst nach etwa 15 bis 20 Sekunden dem langsameren Rad deutlich davonrollt.
Rollversuche auf kurzen Gefällen oder mit relativ kurzem Nebeneinanderherrollen sind also wenig aussagekräftig - eine Erfahrung, die wohl jeder bestätigen kann, der mal Vergleiche beim Nebeneinanderherrollen durchgeführt hat.
(Kleine Denksportaufgabe: Erklären Sie, weshalb die Rollgeschwindigkeit nach Erreichen eines Maximums wieder etwas sinkt, siehe V/t-Diagramm links.)
Inwiefern spielt die Trittfrequenz eine Rolle?
Die Bewegung der Beine beim Treten erhöht den Luftwiderstand.
Die Luftwiderstandskraft wächst quadratisch mit der Geschwindigkeit =>
das Bein, das sich im Tretzyklus jeweils nach vorne bewegt, erhöht den Luftwiderstand mehr, als ihn das andere Bein vermindern kann.
Auch die vertikalen Bewegungen vergrößern den Luftwiderstand, weil sie sich vektoriell zur Fahrgeschwindigkeit hinzuaddieren und vermutlich zusätzliche Wirbel verursachen.
Der Einfluß der Trittfrequenz wird hier mit [ursprüngliches Cd*A] * (1 + Trittfrequenz/500) angenähert.
Weshalb rollt ein schwererer Fahrer schneller bergab?
Das Volumen, und damit die Masse, verhält sich zur Körperoberfläche (und damit Stirnfläche) näherungsweise wie x3 zu x2
=> die Masse wächst schneller als die Stirnfläche
=> beim schwereren Fahrer größere Gewichtskraft auf jedem Quadratzentimeter der Stirnfläche
=> das Gleichgewicht zwischen Hangabtriebskraft und Luftwiderstandskraft wird erst bei höherer Geschwindigkeit erreicht
=> höhere Endgeschwindigkeit.
Auch in der Beschleunigungsphase beim Bergabrollen hat der schwerere Fahrer schon die Nase (Füße) vorn:
in Relation zur Masse kleinere Luftwiderstandskraft läßt, ebenfalls in Relation zur Masse, größere Beschleunigungskraft übrig
=> stärkere Beschleunigung.
("Freier Fall" wäre nur im Vakuum möglich, weil nur dort keine weiteren Kräfte außer der Schwerkraft wirken.
Nur dort fällt eine Feder genauso schnell wie eine Bleikugel, bzw. eine kleine Bleikugel genauso schnell wie eine große.)
Warum sind die Geschwindigkeitsdifferenzen zwischen verschiedenen Rädern beim Bergabrollen größer als in der Ebene?
Weil beim Bergabrollen, gleiches Gesamtgewicht vorausgesetzt, die Antriebskraft identisch ist, beim Treten hingegen die Leistung.
Die zu überwindende Luftwiderstands-Kraft (beim Rollen relevant) steigt mit V2, die aufzubringende Luftwiderstands-Leistung (in der Ebene relevant) hingegen mit V3.
Anschaulicher (unter Vernachlässigung des Rollwiderstands):
Die Hangabtriebskraft ist, gleiches Gesamtgewicht vorausgesetzt, identisch.
Die Räder erreichen jeweils ihre Endgeschwindigkeit, wenn die mit V*V wachsende Luftwiderstandskraft so groß wie die Hangabtriebskraft geworden ist (Kräftegleichgewicht - vorher dient der übrige Teil der Hangabtriebskraft der Beschleunigung).
Das aerodynamisch bessere Rad, mit geringerer Luftwiderstandskraft bei gegebenem V, erreicht dieses Kräftegleichgewicht erst bei höherer Geschwindigkeit und ist damit schneller.
Weil aber die erforderliche Leistung schneller (mit V*V*V) als die Kraft (mit V*V) wächst, kann das aerodynamisch bessere Rad in der Ebene (gegebene Leistung) weniger Geschwindigkeitsvorteil herausholen als beim Rollen (gegebene Kraft).
Anmerkung:
Die Gravitation muß zwar beim Rollen (Endgeschwindigkeit) für das schnellere Rad mehr Leistung aufbringen, weil: Leistung = Kraft * V, Kraft identisch, V aber größer.
Aber sie könnte, im Gegensatz zum Fahrer, ihre Leistung beliebig steigern, nur ihre Kraft bleibt konstant (jedenfalls innerhalb von kosmologisch vernachlässigbaren Zeit- und Raumveränderungen *g*).
Weshalb ist der Leistungsbedarf bei starkem Gefälle zwischen den verschiedenen Rädern so extrem unterschiedlich?
|
Beispiel: Gefälle 14%, Höhe über NN 1000 m, Trittfrequenz 150/min, sonstige Werte wie voreingestellt, Geschwindigkeit 90 km/h: |
|||
| Rennrad Obenlenker-Haltung | 1389 Watt | ||
| Rennrad Untenlenker-Haltung | 48 Watt | ||
Antwort:
Weil die für diese Geschwindigkeit nötige Gesamtleistung sehr hoch ist und der
größte Teil davon von der Schwerkraft "erbracht" wird. Die Differenz
von 1341 Watt, die am Fahrer hängen bleibt, ist im Vergleich zur Gesamtleistung
relativ klein. Der Leistungs- und Geschwindigkeitsrechner auf www.kreuzotter.de errechnet nur die Fahrerleistung.
Warum ist den verschiedenen Rädern nicht jeweils ein bestimmtes, festes Cd * A ("effektive Stirnfläche") zugeordnet?
Die Stirnfläche des Fahrers ergibt sich individuell unterschiedlich aus Gewicht und Größe. Größeres Gewicht bedeutet größeres Volumen und damit mehr Stirnfläche (außer in den vollverschalten HPV).
Dabei wird die Sitzposition als Neigung von Oberkörper, Armen und Beinen zur Horizontalen berücksichtigt.
Hinzu kommt die effektive Stirnfläche des Fahrrades selbst,
die wiederum vom gewählten Reifentyp via Breite und Profil beeinflußt wird.
Die Auswirkung der Trittfrequenz auf die Aerodynamik wird hier mit [ursprüngliches Cd*A] * (1 + Trittfrequenz/500) angenähert.
Und wie wird die Stirnfläche des Fahrers aus Körpergewicht und -Größe berechnet?
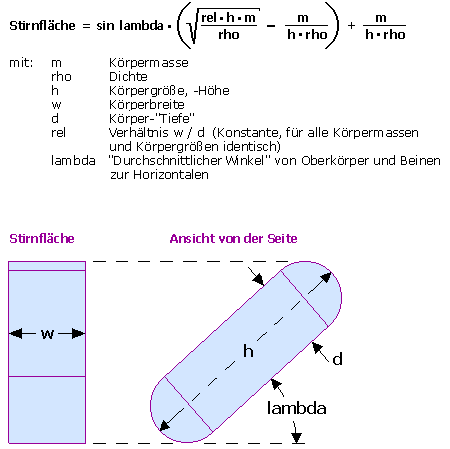
Der Körper wird zu einem Quader mit oben und unten aufgesetzten Halbzylindern (siehe Bild) vereinfacht.
Die Halbzylinder simulieren am realistischsten, daß die Höhe der Stirnfläche sofort abnimmt, sobald die absolut aufrechte Körperposition (90 Grad aufrecht stehender Mensch) verlassen wird (Kopf, Schultern, Nates sind ja auch eher rund als eckig).
Der Winkel lambda des Quaders zur Horizontalen spiegelt den Durchschnitt der Winkel von Oberkörper, Armen und Beinen auf dem jeweiligen Radtyp wieder.
Dabei werden die Winkel von Oberkörper/Beinen/Armen wie 8/6/3 gewichtet.
Warum sind die ausgegebenen Cr-(Rollwiderstands-)Beiwerte so niedrig?
Weil das Programm dabeben auch den dynamischen, geschwindigkeitsabhängigen Rollwiderstand CrV berücksichtigt.
Das heißt, es teilt die Rollwiderstandskraft in einen konstanten und einen dynamischen Anteil auf.
In dem Zahlenfeld ausgegeben wird nur der Beiwert für den konstanten Anteil.
Wie entsteht der dynamische, geschwindigkeitsabhängige Rollwiderstand (Beiwert CrV)?
Unmittelbar vor der abgeplatteten Radaufstandsfläche des Reifens bewegt sich die Lauffläche immer noch vertikal relativ zum Boden (mit V*sin(Winkel_der_Lauffläche_zum_Boden)).
Diese vertikale Bewegung wird am vorderen Rand der Radaufstandsfläche abrupt beendet, die Lauffläche "klatscht" auf den Boden
=> die kinetische Energie, die im jeweils betroffenen Teil der Lauffläche steckte, geht verloren (als Wärme in den Boden und in die Lauffläche).
Strenggenommen folgt daraus, dass auch der dynamische Rollwiderstandsbeiwert mindestens abhängt von:
Reifeninnendruck, Laufraddurchmesser, Dicke und spezifischem Gewicht (bzw. Masse/Umfang) der Lauffläche,
und von der Normalkraft, durch die der der Reifen abgeplattet wird.
Also von allen Parametern, die bestimmen: Wie viel Masse trifft am vorderen Rand der Aufstandsfläche auf dem Boden auf, und in welchem Winkel, also mit welcher vertikalen Restgeschwindigkeit (je nach Fahrgeschwindigkeit).
Die Annahme "Dynamischer Rollwiderstandbeiwert = 0.1*cos(Fahrbahnsteigungswinkel)" des Geschwindigkeits-Leistungs-Rechners ist also eine vereinfachende Approximation, insbesondere die Gewichtskraft wird (momentan noch) vernachlässigt.
Anmerkung: Im Vergleich zum KFZ spielt beim Fahrrad der dynamische Rollwiderstand vermutlich eine geringere Rolle, da Fahrradreifen leichter sind und i.d.R. einen höheren Innendruck aufweisen.
Wenn ich die Leistung bei Gefälle ausrechne und als Diagramm zeichnen lasse: Woher kommt die Unstetigkeit an der Nullstelle (siehe Bild)?
 Der Fahrer hört bei Leistung = 0 (freies Rollen) zu treten auf. Das Programm geht jedenfalls davon aus.
Somit sinkt der Luftwiderstand.
Um nicht wieder etwas schneller zu rollen als unmittelbar oberhalb der 0-Watt-Grenze, wo der Luftwiderstand trittfrequenzbedingt höher war, muß der Fahrer sofort leicht zu bremsen beginnen, das heißt negative Leistung aufbringen.
Der Fahrer hört bei Leistung = 0 (freies Rollen) zu treten auf. Das Programm geht jedenfalls davon aus.
Somit sinkt der Luftwiderstand.
Um nicht wieder etwas schneller zu rollen als unmittelbar oberhalb der 0-Watt-Grenze, wo der Luftwiderstand trittfrequenzbedingt höher war, muß der Fahrer sofort leicht zu bremsen beginnen, das heißt negative Leistung aufbringen.
Geändert: 28.9.2008 Impressum / Über diese Seite